KONUKLARINIZIN SESİ 382

0

BEĞENDİM

ABONE OL

News

0

            AYT MATEMATİK SORULARINA NASIL HAZIRLANRIZ?

            AYT matematikte, 1) Aritmetik, 2) Cebir, 3) Geometri, 4) Analitik geometri, 5) Fonksiyon grafiği, 6) Trigonometri, 7) Ölçüm bilgisi, 8) Olasılık-düzenleme, 9) İstatistik, 10) Küme bilgisi, 11) Mantık, 12) Karmaşık sayılar, 13) Vektörel hesap, 14) Analiz (limit-türev-integral), 15) Özel simgeleme diye onbeş konudan sorular soruluyor.

            Diğer kaynaklarda bu sınıflandırma yapılmadığı için AYT matematiğine hazırlanmayı hem kolaylaştıracak, hem anlamlı kılacak bu sınıflandırmayı özetle ve genelde açıklayalım.

            (1) Aritmetik-Cebir-Analiz birlikte bir matematik dalı, Sayı Bilgisi. Aritmetikte doğal sayılarla, bunlara eksi sayıları ekleyerek tamsayılarla, kesirleri ekleyerek rasyonel sayılarla, bunlarla farklı belirlenen ve sonlu kesirlerle ancak yaklaşık gösterilebilen irrasyonel sayıları ekleyerek gerçel sayılarla 9 işlem (toplama, çarpma, üs alma, bunların karşıtları; çıkarma, bölme, kök alma, logaritma ve iki özel işlem çarpınım (faktöriyel), toplanım (binom katsayısı) yapıyoruz ve aralarında iki bağıntı (eşitlik ve eşitsizlik) kuruyoruz.

            Cebirde, harf kullanarak genelleme yapıyor ve böylece özdeşliklerde tüm genel bağıntıları belirliyoruz. Fonksiyonlarda, sayılar arasında genel bağıntılar kuruyor ve böylece bilimlerdeki tüm doğal bağıntıları simgeleştirebiliyoruz. Denklemlerde, fonksiyonlara ek bilgi ekleyerek diğer değişkenleri bilinmeyen kılıyor ve değerlerini buluyoruz.

            Analizde, gerçel sayılarımıza iki özel sayı; çok çok küçük ama yok da değil karşılığı limit sıfırını (cebirde dx…) ve çok çok büyük sonsuzu (simgesi ¥, cebirde 1/dx) ekliyor ve bunlarla işlemler yapıp, bağıntılar kurarak limit bilgisini oluşturuyoruz. Türev, (fonksiyonda çok küçük değişimlerin fonksiyonu ve bilimin gelişmesini sağlayan) özel bir limit; integral türevin karşıtı.

            (2) Geometri, faklı bir matematik dalı; Konum Bilgisi.  Geometriyle düzlemde veya uzayda konum belirliyoruz. Geometrik şekiller (nokta, doğru, açı, üçgen, çember…) birbirleriyle konumsal bağıntılı nokta kümeleri.

            (3) Analitik geometri, fonksiyon grafiği, trigonometri, ölçüm bilgisi, ACA (Aritmetik-Cebir-Analiz) ve geometri arasında aktarmalar. Analitik geometride geometriyi ACA’ya; fonksiyon grafiğinde de ACA’nın fonksiyonunu geometriye; trigonometride geometrinin açısını ACA’ya; ölçüm bilgisinde geometrinin uzunluk, alan, hacim kavramlarını sayısallaştırarak ACA’ya aktarıyor ve böylece çözümlerimizi kolaylaştırıyoruz.

            (4) Olasılık, ACA’yı kullanan yeni bir matematik dalı; Beklenti Bilgisi. Düzenlemeler ve İstatistik olasılık uygulamaları.

            (5) Küme bilgisi, tüm diğer matematik dallarının genellemesiyle oluşturulmuş ve hiçbir özelliği olmayan ögeler matematiği.

            (6) Mantık, iletişimden soyutlanmış (dilleri çok kısıtlı kapsayan) bir matematik dalı: Bildiri Bilgisi.

            (7) Vektörel hesap, konum belirlemeyi geliştirip kolaylaştıran bir analitik geometri.

            (8)  Karmaşık sayılar, ACA’ya

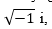
sanal ve tek özelliği karesinin -1 olduğu bilinen bir sayının eklenmesiyle oluşturulmuş bir özel ACA’nın ögeleri.

            (9) Özel simgeleme, adı üzerinde.

            Şimdi (TYT matematik sorularına nasıl hazırlanalım? da anlattığımız gibi) AYT matematiğe hazırlanırken,

            a) Dershaneye giderek, özel ders alarak, soru bankası… kullanarak ÇÖZÜM EZBERLEME’yi seçersek başarılı olmamız çok zor. Ne öğrendiğimizi bilmeden birçok matematik dalının uygulaması olan problemlerin çözümünü ezberlememiz gerekli. Üstelik bazı AYT soruları ya soyutlaştırılarak, ya karmaşıklaştırılarak özellikle zorlaştırılmış. Buna ek, bizim ezberlediğimiz çok sayıda benzer soruyla sınavda çözmemiz gereken sorular arasında bağ kurarak doğru şıkkı işaretleyebilmemiz gerekli. Son söylediklerimizi 2025 AYT matematik sorularını irdeleyerek somutlaştıralım.

            2025 AYT sorularında, yukarıda bizim verdiğimiz sınıflandırmadaki matematik dallarında sorulan AYT sorularının bir bakıma daha özel bilgilerinden oluşturduğumuz 65 soru tipinden 31 i kullanılmış. Ama bazı sorularda birden fazla tip bilgisi kullanılarak. (Bu 65 soru tipini matematik ezberini azaltmak için oluşturduk. 2018~2025 deki 8 AYT sınavını irdeleyerek oluşturduğumuz bu soru tiplerini isteyene elmekle göndeririz.) 2025 AYT matematik sorularından,

             (1) 13 soru TYT bilgisiyle bile çözülebilir. Düzlemde ölçüm bilgisi sorularını buraya kattık. Bu tür çok çözüm ezberlediysek bu tür her soruyu kolayca çözebiliriz.

             (2) 16 soruda (logaritma, trigonometri, analiz genel bilgileri gibi) ek bilgiler gerekli. Çözüm ezberleyerek bu tür soruları nasıl çözebileceğimizi biz bilemiyoruz. Logaritma özdeşliklerinde çok sayıda çözüm ezberlersek sınavda bize sorulan doğru şıkkı işaretlememiz belki olanaklı. Çünkü bunların genel bilgisi kısa. Bazı limit sorularında da hep aynı çözüm uygulandığından benzetme kolay. Genel bilgisi öğrenirsek her türevi kolayca alabiliriz. Bu nedenle çok sayıda çözüm ezberleyerek de başarıya ulaşılabiliriz. Ayrıca ‘konu anlatımı’ adıyla, düzensiz de olsa genel bilgi veriliyor. İntegral sorularını çözebilmemizse sorulan soruların basitliğine bağlı.

             (3) 10 soruyu zor bulduk, neden? Bu soruların bazılarında işlem çok, hem hızlı yapmak, hem de arada hata yapmamak gerekli. Bazıları özel değer matematiği, yani genelde ya çözümsüz, ya da genel çözümü uzun zaman gerektiriyor. Bu tür sorulara alışkın olmak, özel değerlerle çözümü hemen algılayıp çözmek gerekli. Ancak bu sorulara çok benzer soru çözümü ezberlemişler bu soruları pek de düşünmeden çözebilirler.

             (4) Bir olasılık sorusunun verilen çözümü yanlış. Ama ilginç, internette soruları çözenler de bu yanlış çözümü yineliyor.

              Sonuç: Çözüm ezberleyerek 2025 AYT sorularının tümünü veya tümüne yakınını çözen çocuklarımızın bunu nasıl başardığını bilemiyoruz.

              b) Yukarıdaki sınıflandırmaya göre MATEMATİK ÖĞRENEREK AYT matematiğine hazırlanmamız başlangıçta bize daha zor gelecek. Ama çok daha az çalışarak ve çok daha az ezberle başarılı olabiliriz. Üstelik başarımız kesin. Ama verilen sürede soruların tümünü çözmeyi de hedeflemeyebilir ve özellikle özel değer matematiği sorularıyla veya çok karmaşık olanlarla uğraşmayabiliriz.

             AYT matematiğinde hedefi daha alçak gönüllü (15~25 çözüm) olanlar için (belki biraz daha sınırlama yaparak) matematik öğrenmek çok akıllıca.

                                                                                                                               Sağlıcakla,